Задача : Дзета 6.9
Окружность девяти точек
Известно:
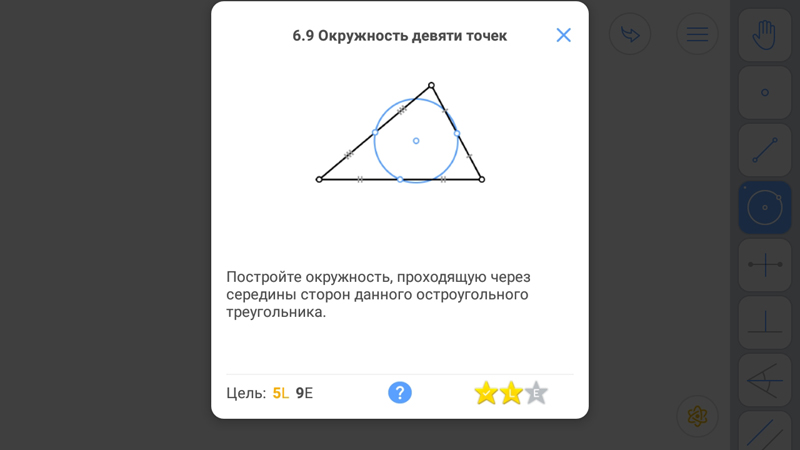
Окружность девяти точек — это окружность, проходящая через середины всех трёх сторон треугольника.
Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности.
Ортоцентр — точка пересечения высот треугольника или их продолжений.
Воспользуемся вторым утверждением. Опустим две высоты.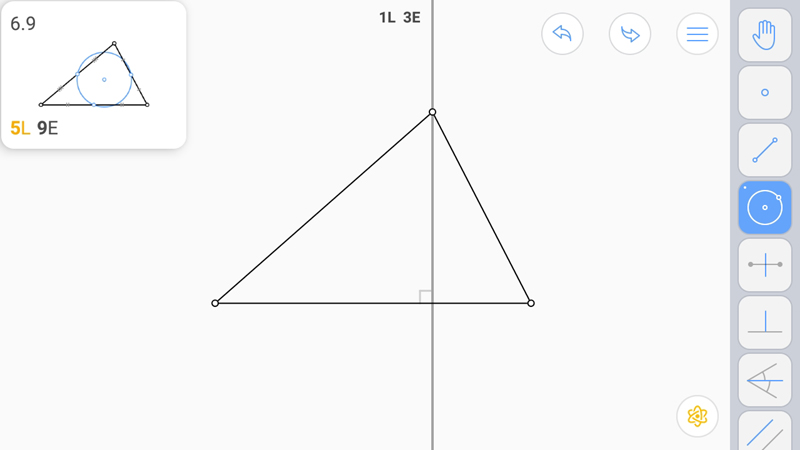
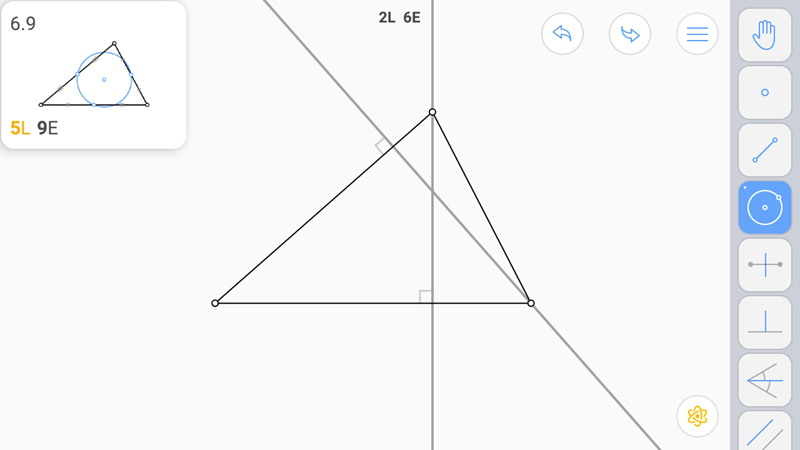
Построим серединные перпендикуляры, их пересечение даст центр окружности.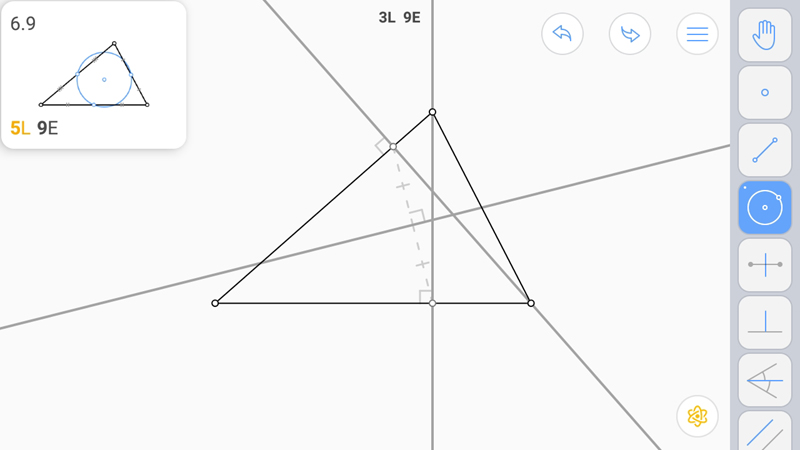
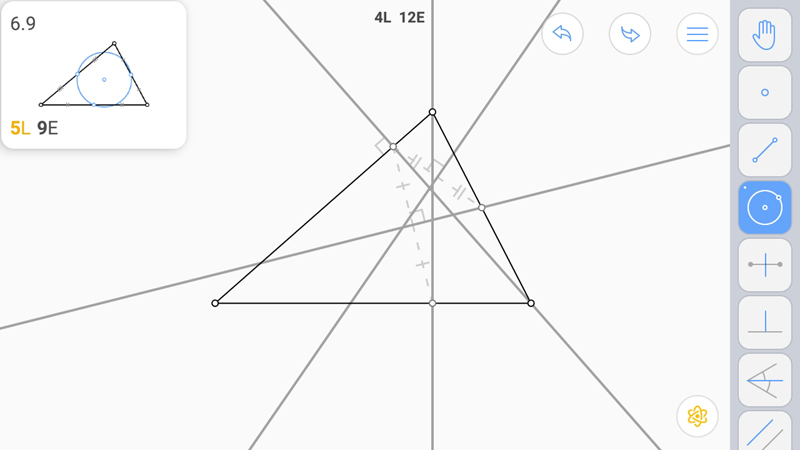
И построим окружность.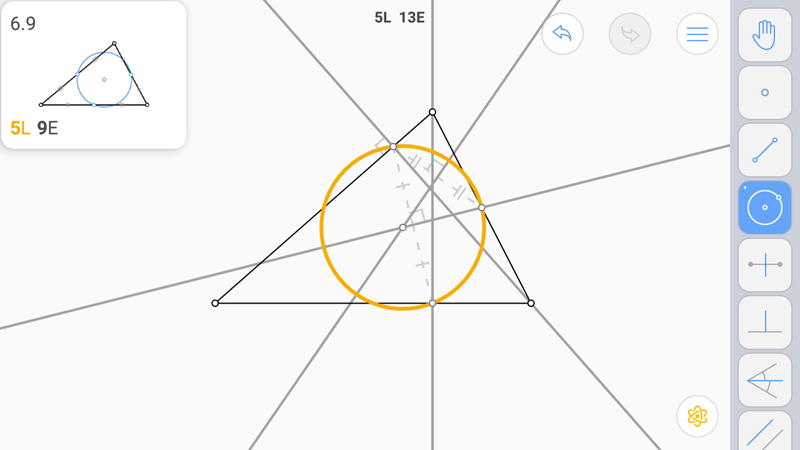
L-звезда.
slider_L
E-звезду строим так. Серединный перпендикуляр к стороне.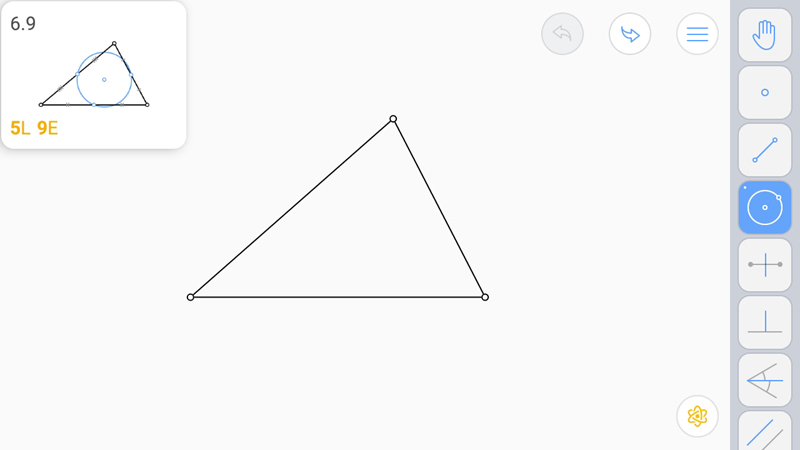
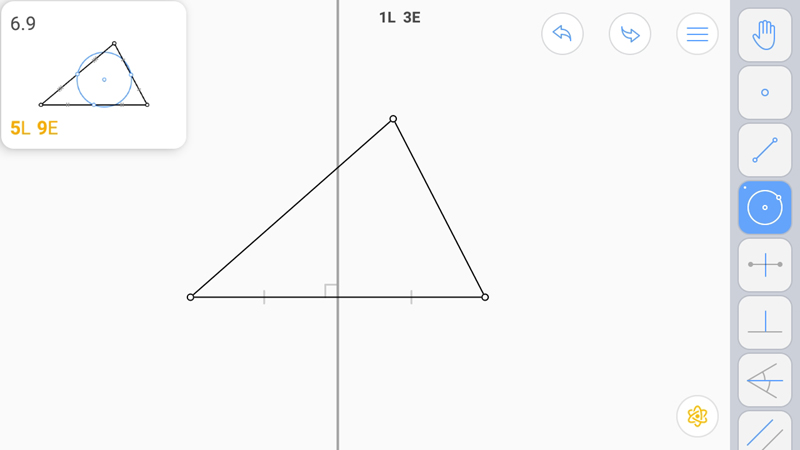
Окружность из середины.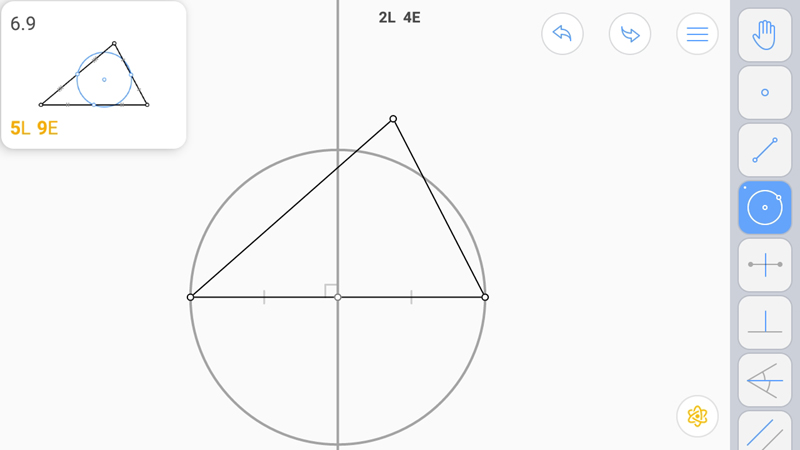
Встречная окружность из точки пересечения окружности со стороной.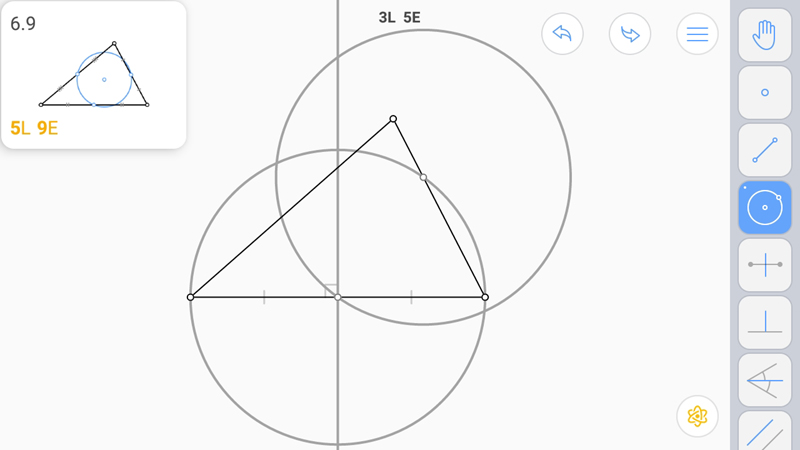
Прямая через точки пересечения окружностей.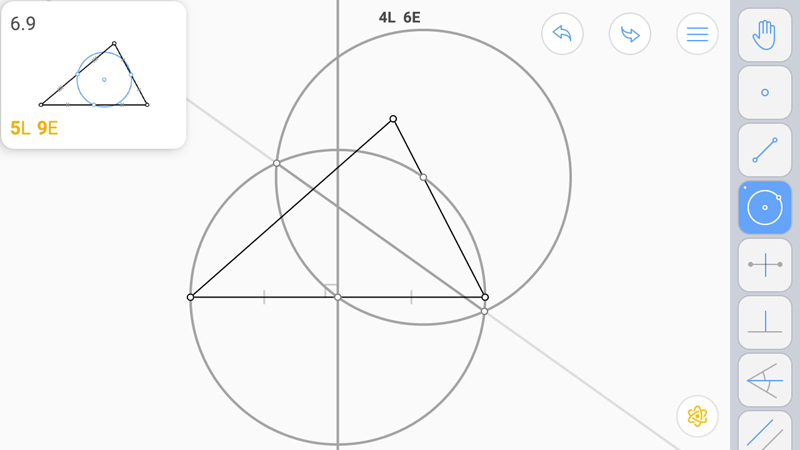
Повторить для другой стороны.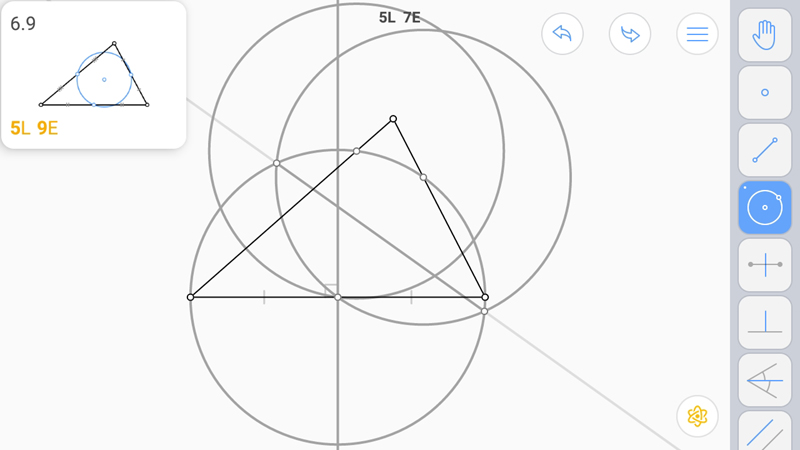
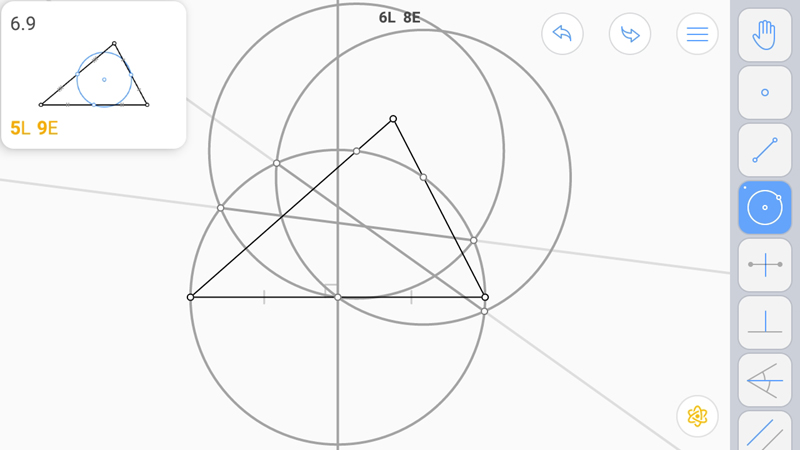
Точка пересечения прямых - центр окружности девяти точек.
E-звезда. Почему такое построение верно, не знаю.
Окружность девяти точек единственная.
slider_E

