Задача : Гамма 3.9
Центр четырехугольника
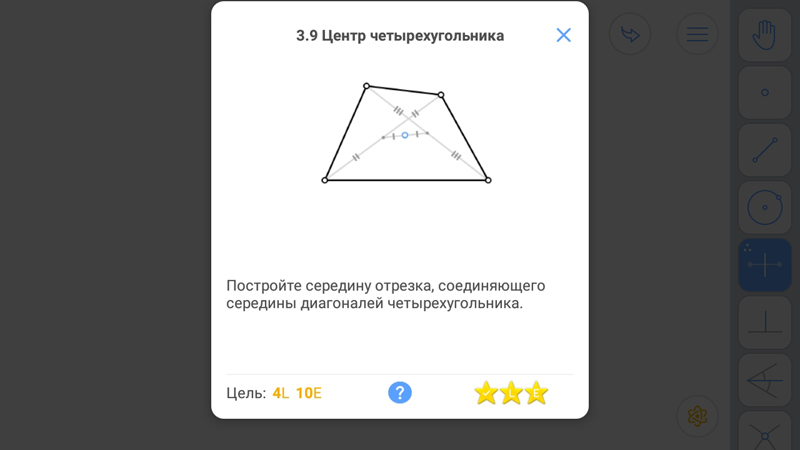
Известно:
Теорема Гаусса.
Если в четырёхугольнике две пары противоположных сторон не параллельны, то две середины его диагоналей лежат на прямой, которая проходит через середину отрезка, соединяющего точки пересечения этих противоположных сторон. Указанная прямая называется прямой Гаусса.
Известно:
Два отрезка, соединяющих середины противоположных сторон четырехугольника называются первой и второй средними линиями четырёхугольника. Также их называют бимедианами. Отрезок, соединяющий середины диагоналей четырехугольника называется третьей средней линией четырёхугольника.
Известно:
Обобщённая теорема Ньютона.
Все три средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам.
Построим серединные перпендикуляры к противоположным сторонам.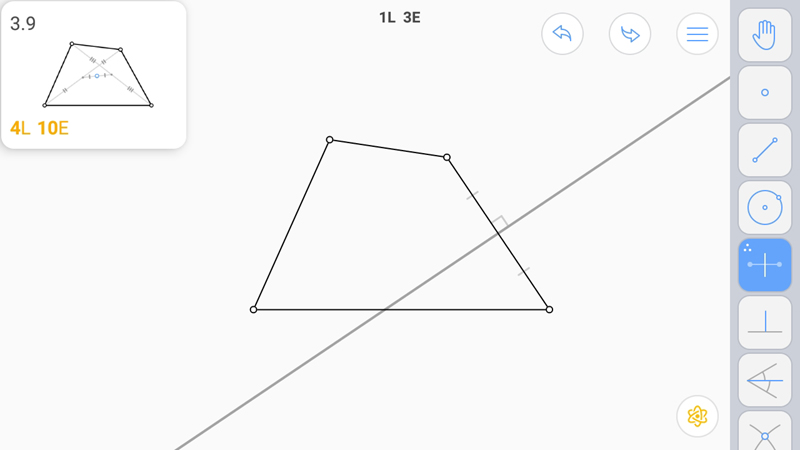
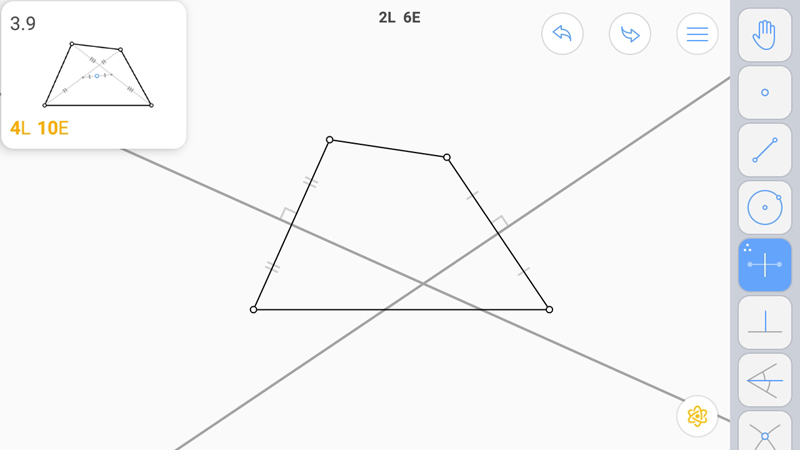
И середина из середин.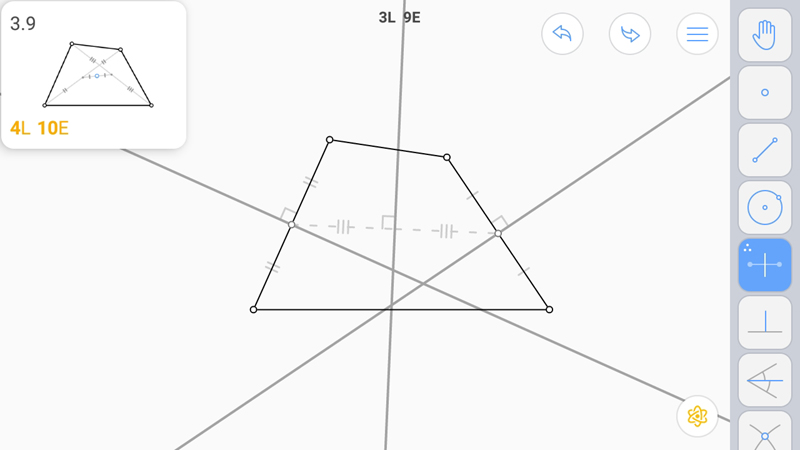
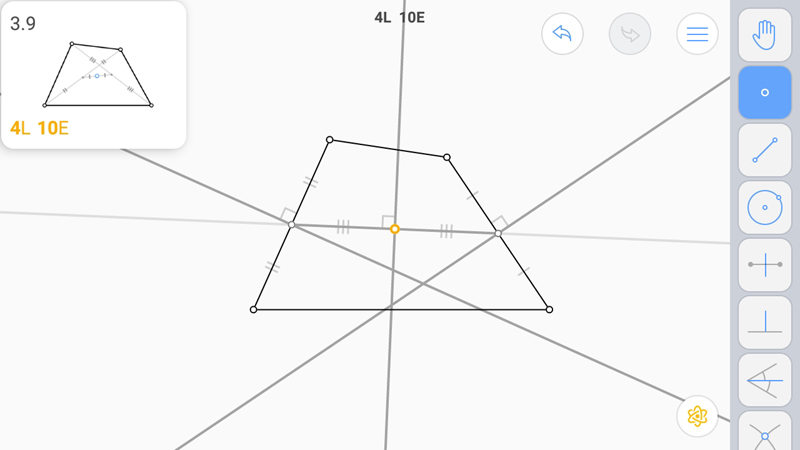
L и E звезды. Решение единственное, центр один.

