Задача : Гамма 3.5
Окружность через точку, касающаяся прямой
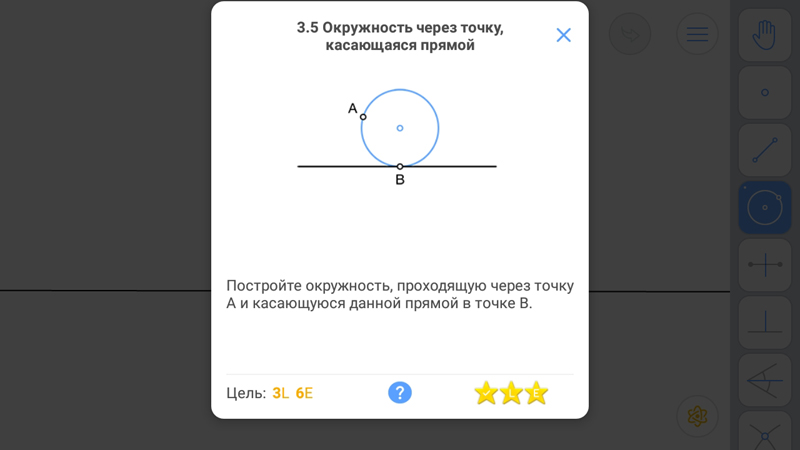
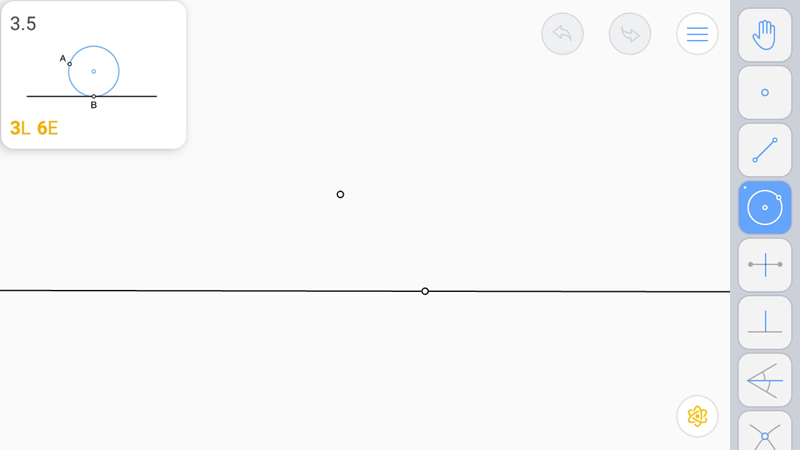
Известно:
Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде.
Если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам.
Радиус окружности, проведённый через точку касания касательной, перпендикулярен касательной прямой.
Перпендикуляр к радиусу в точке на окружности является касательной прямой.
Построим перпендикуляр к касательной.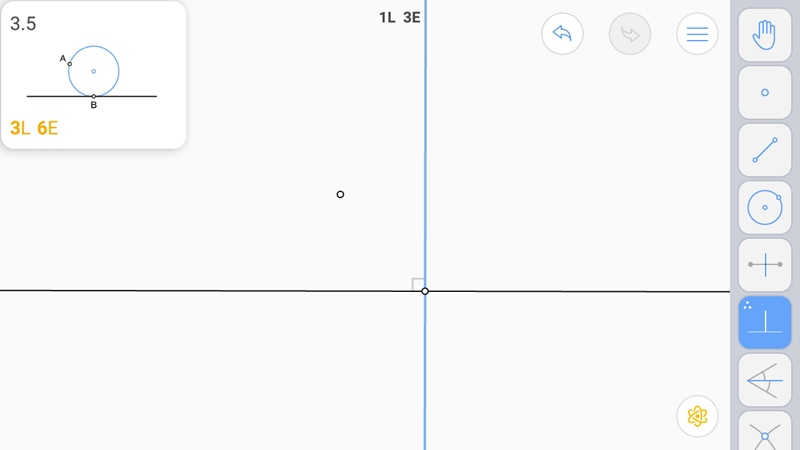
A и B сидели на "трубе". Построим серединный перпендикуляр к несуществующей хорде AB.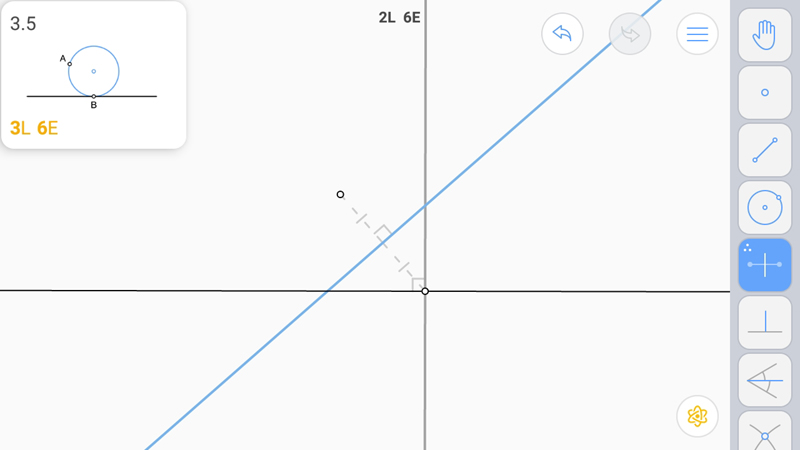
Точка их пересечения будет центром "трубы".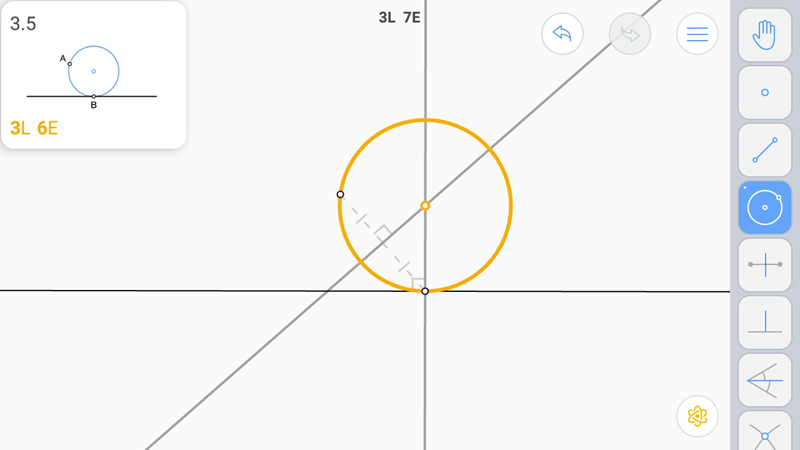
L-звезда.
slider_L
E-звезду опять построим совместным использованием окружностей.
Восстановим перпендикуляр как в 2.7.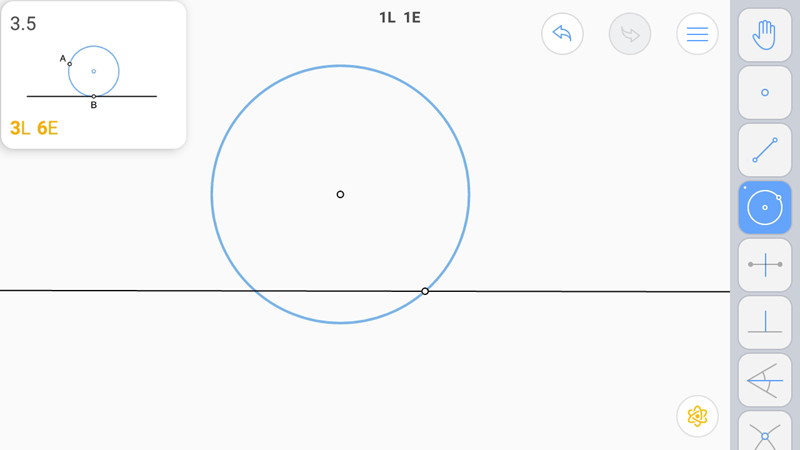
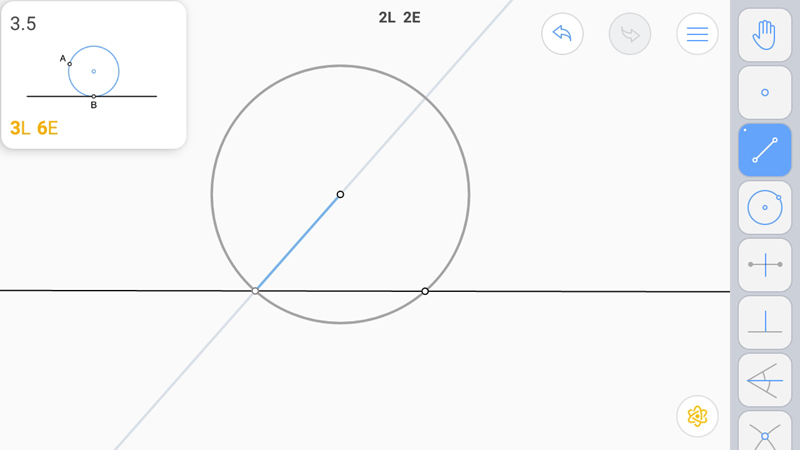
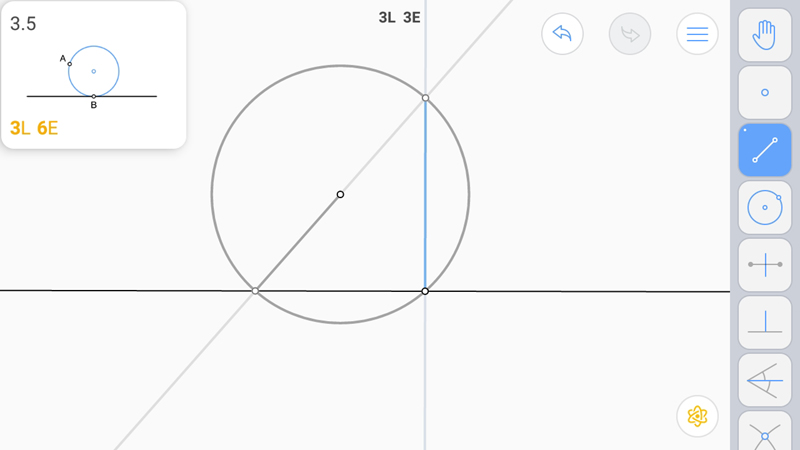
И построим серединный перпендикуляр. При этом одна окружность уже есть.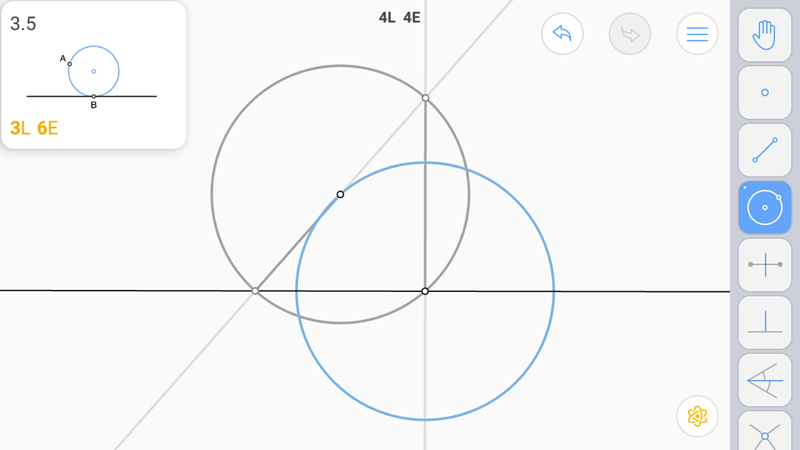
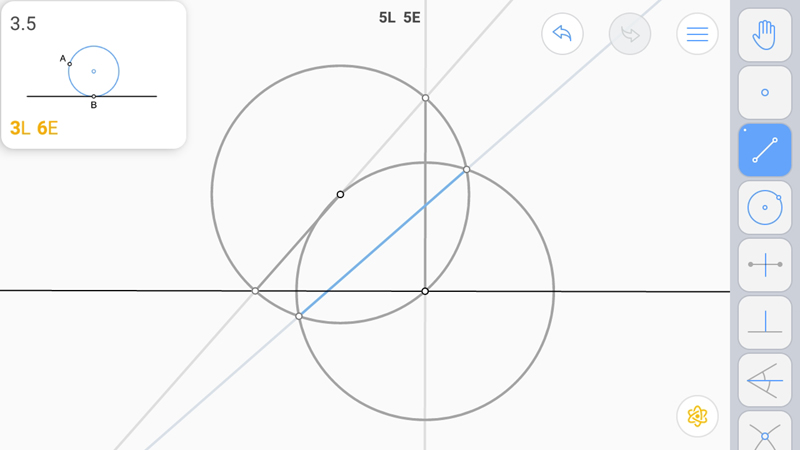
Искомая окружность.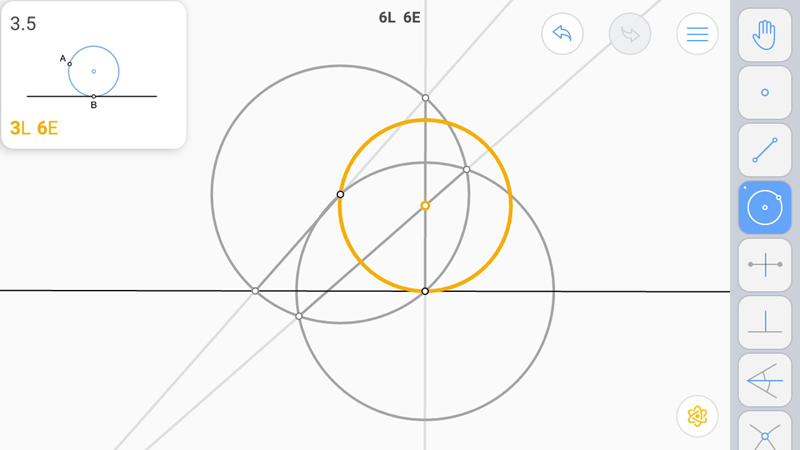
E-звезда. Решение единственное.
slider_E

