Задача : Бета 2.8
Касательная к окружности в точке
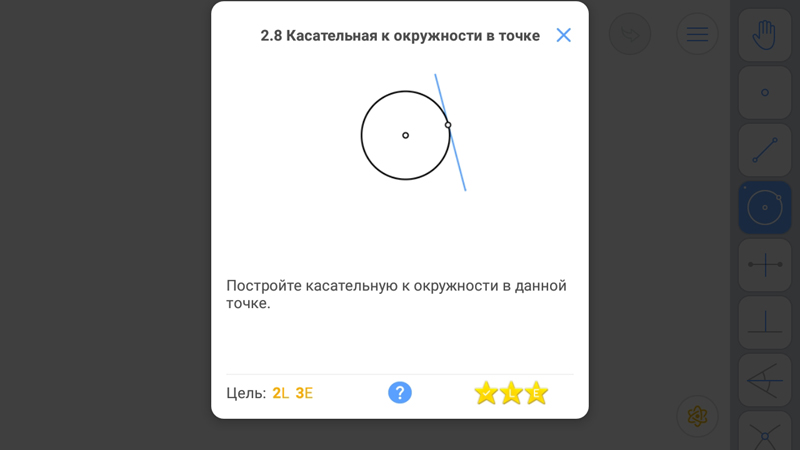
Известно:
Радиус окружности, проведённый через точку касания касательной, перпендикулярен касательной прямой.
Перпендикуляр к радиусу в точке на окружности является касательной прямой.
Воспользуемся вторым определением. Проведем радиус в исходную точку.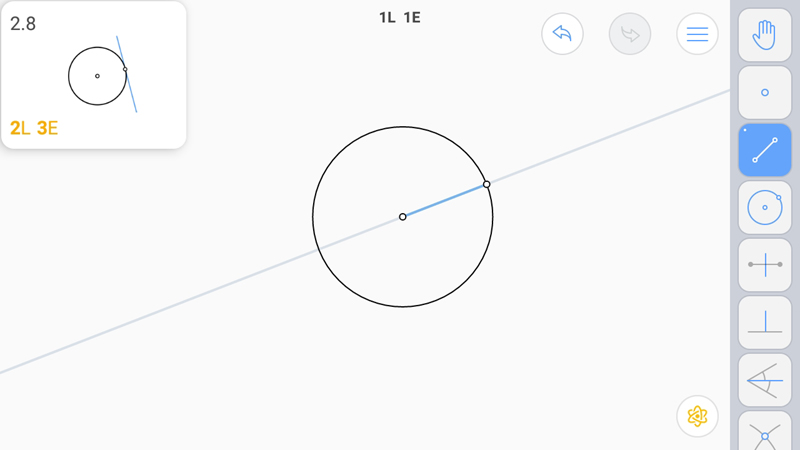
И перпендикуляр.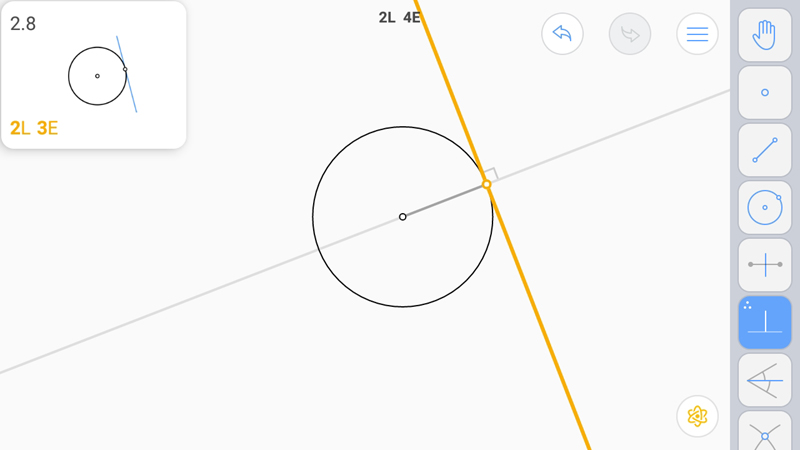
L-звезда.
slider_L
Построение E-звезды не очевидно. Подсказка сообщает следующее.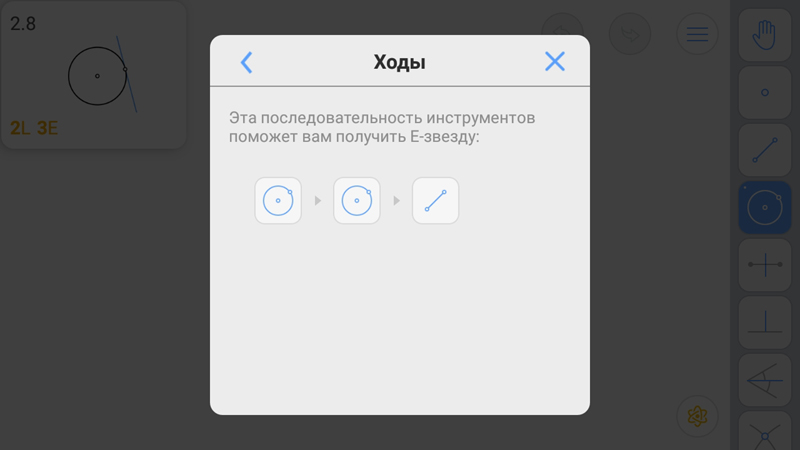
И даже в этом случае построить непросто. Вновь помогает окружность, построенная на точках пересечения окружностей.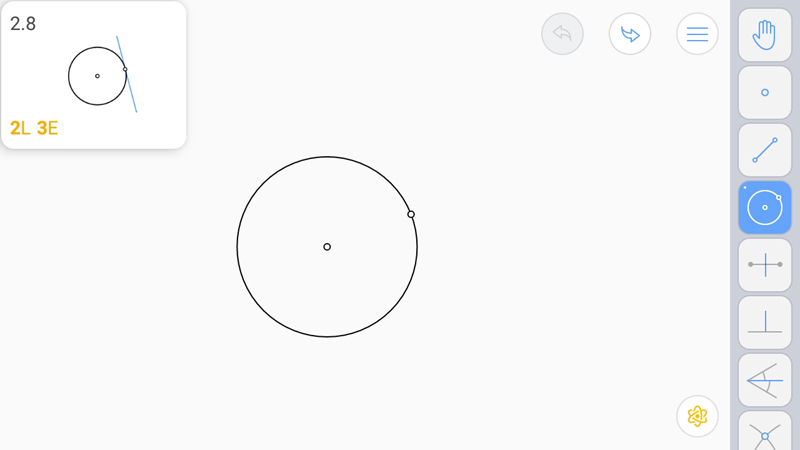
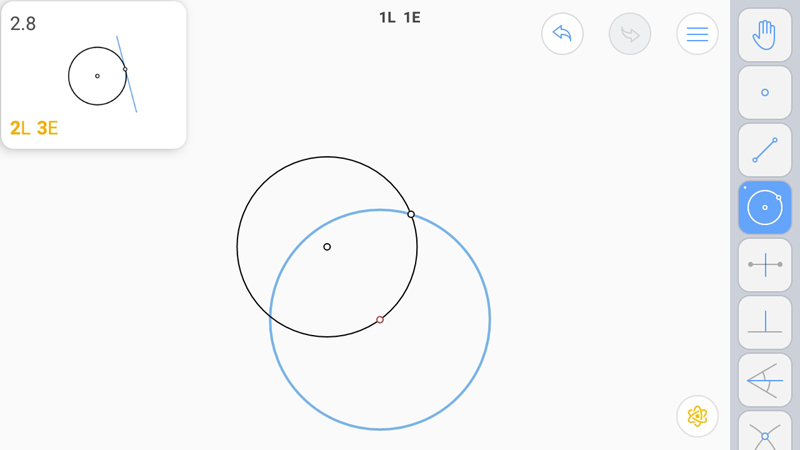
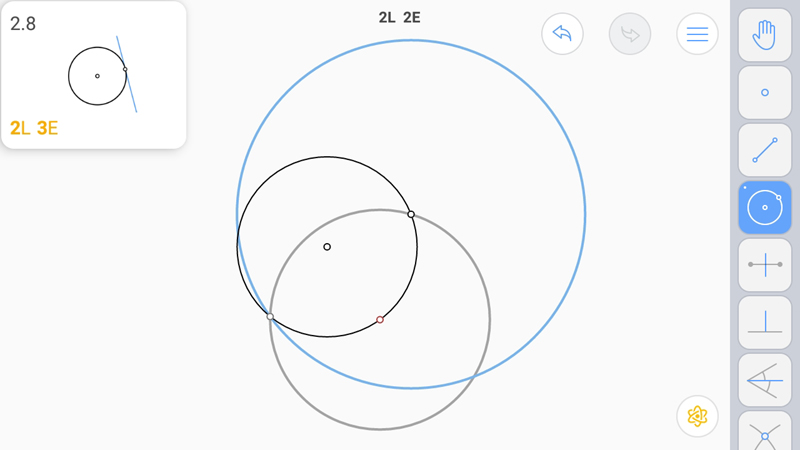
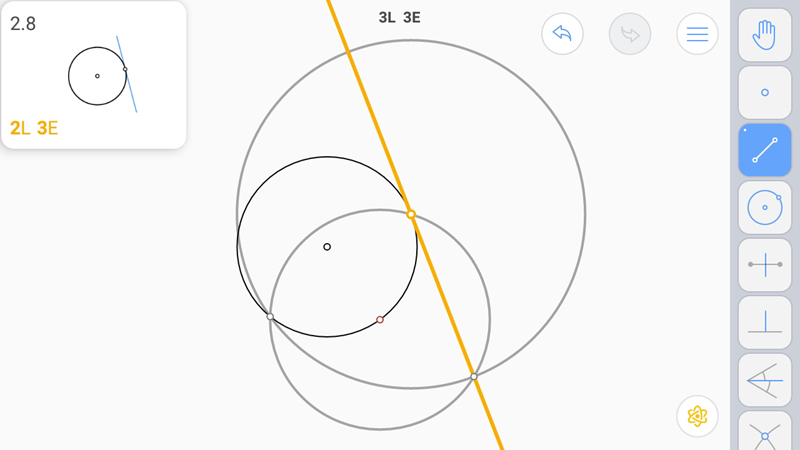
E-звезда. Понятно, что касательная в точке единственная.
slider_E
Попытка обоснования.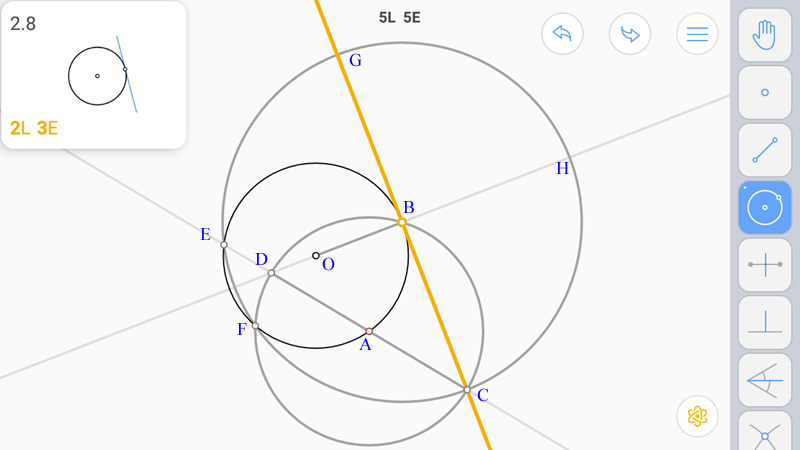
Проведем прямую OB. Задача свелась к 2.7. Окружность AB пересекает ее в точке D. Проведем прямую AD. Она пересечет окружность AB в точке С. Поскольку имеем вписанный угол DBC, опирающийся на диаметр, то он прямой. Если провести AB, то можно увидеть, что окружность B откладывает равные дуги BC и BF. То есть B лежит на серединном перпендикуляре к хорде CF. Но серединный перпендикуляр проходит через центр, то есть является AB. Зато теперь не доказано, что окружность BC пересекает окружность OB в точке F. Надо подумать.

