Задача : Бета 2.10
Окружность, вписанная в ромб
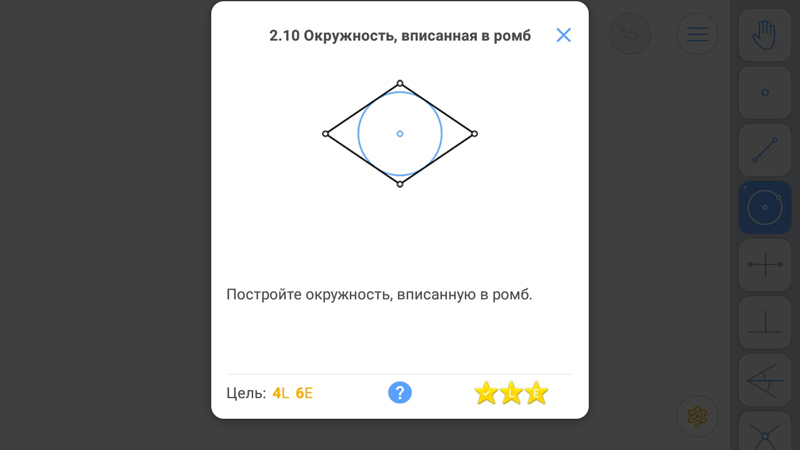
Известно:
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех внутренних углов данного многоугольника пересекаются в одной точке, которая и является центром вписанной окружности.
Диагонали ромба являются биссектрисами его углов.
В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Построим диагонали.
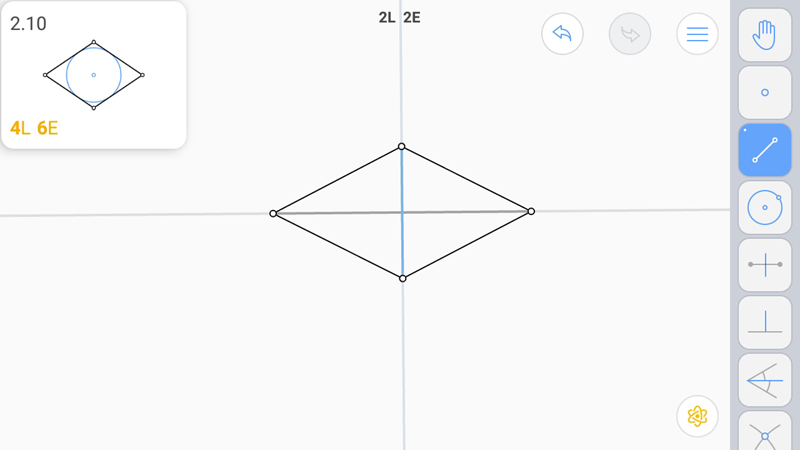
Точку касания найдем построением перпендикуляра к стороне из точки пересечения диагоналей.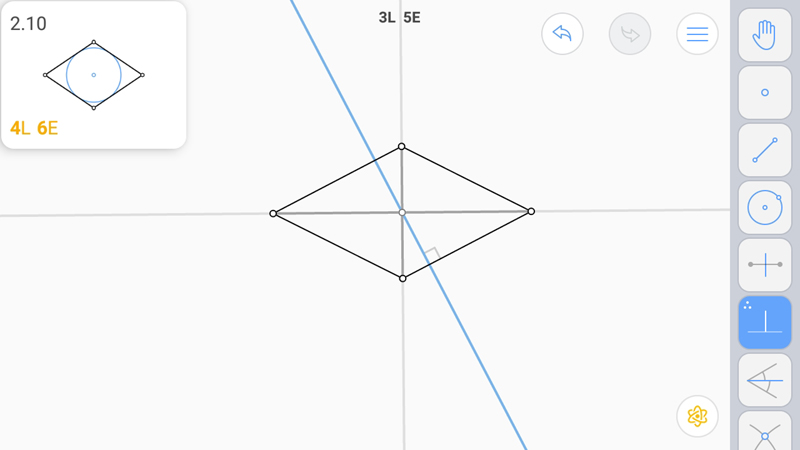
И построим окружность.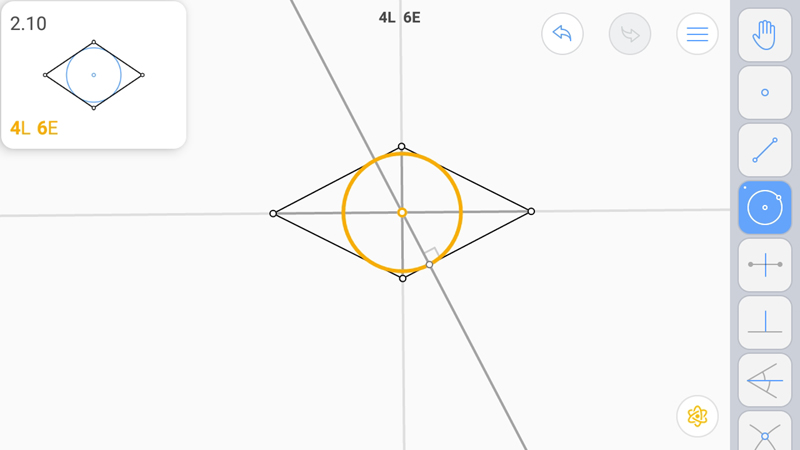
L и E звезды. Решение единственное.
slider_L

