Задача : Мю 12.5
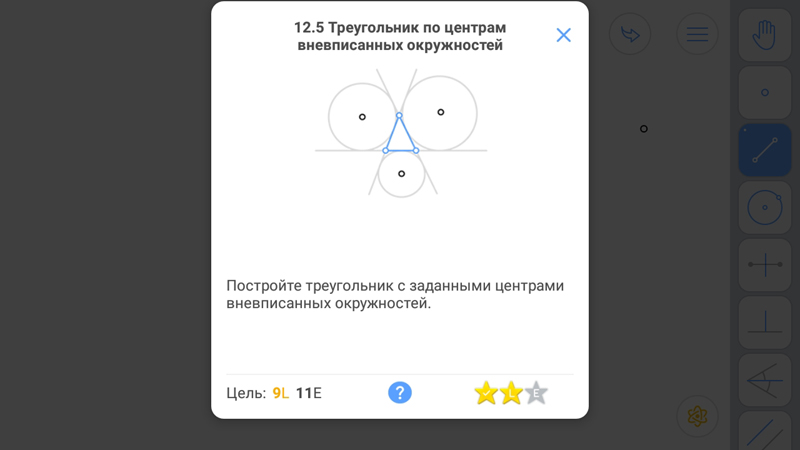
Треугольник по центрам вневписанных окружностей
Известно:
Вневписанная окружность треугольника — окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон. У любого треугольника существует три вневписанных окружности.
Биссектрисы двух внешних углов треугольника и биссектриса внутреннего угла, не смежного с этими двумя, пересекаются в одной точке, которая и является центром такой окружности.
Треугольник является ортотреугольником для треугольника, построенного на вершинах вневписанных окружностей.
Построим прямую, соединяющую центры вневписанных окружностей и перпендикуляр к ним.
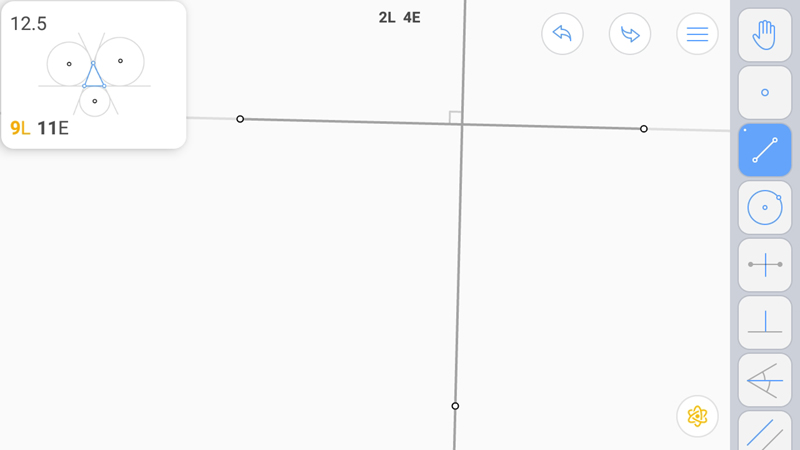
Получили вершину.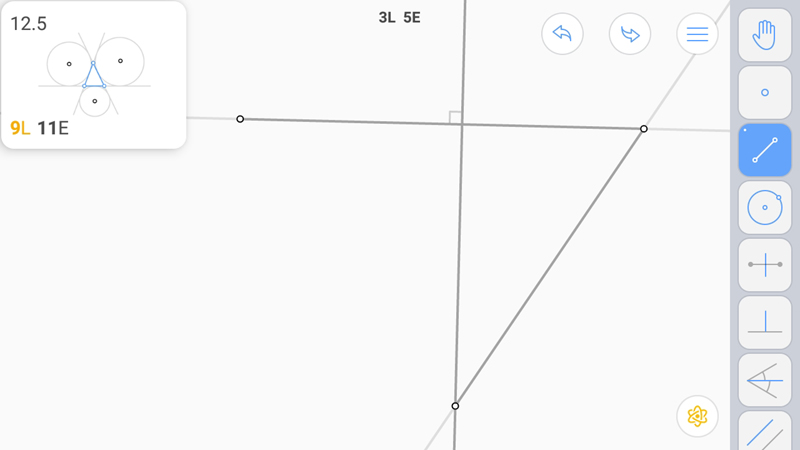
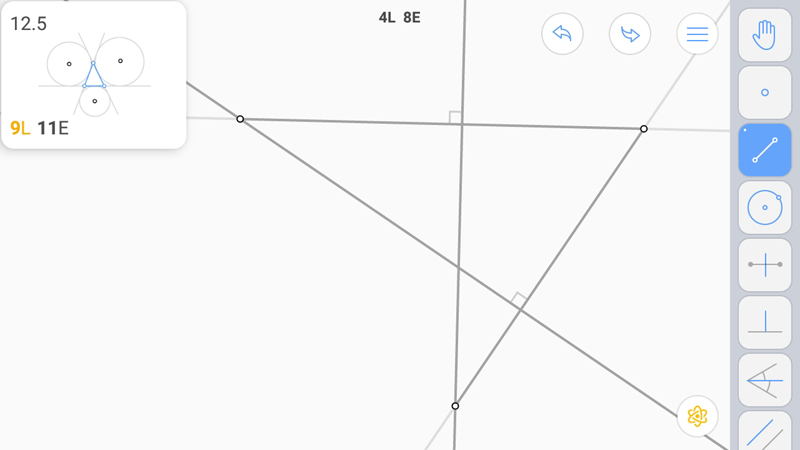
Вторую.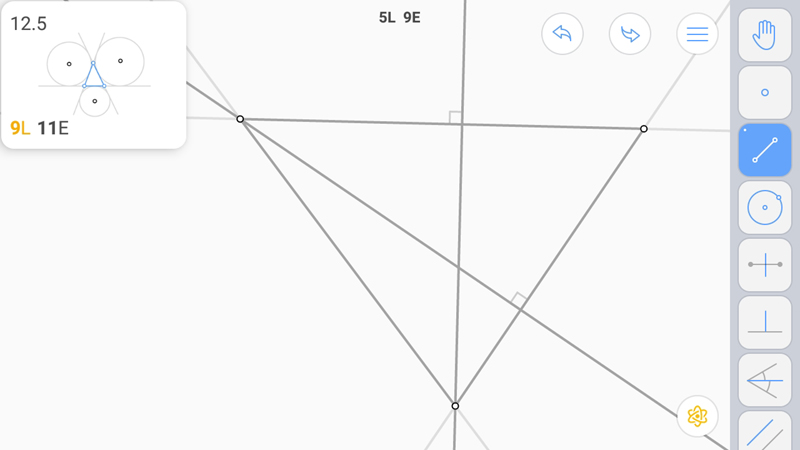
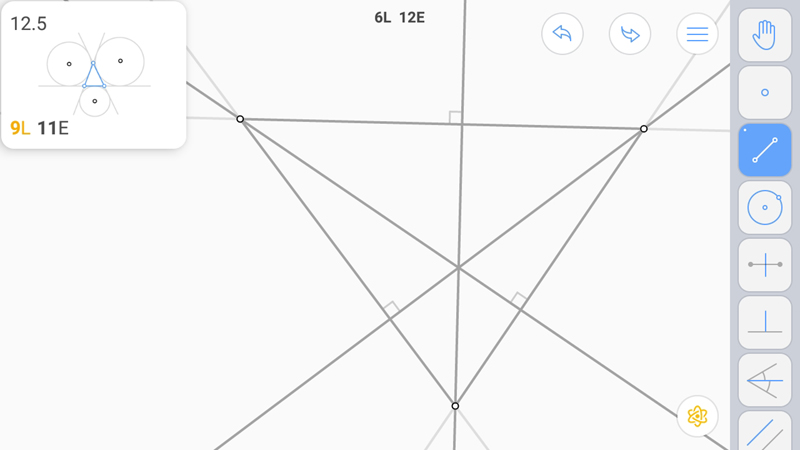
Третью. Построим треугольник.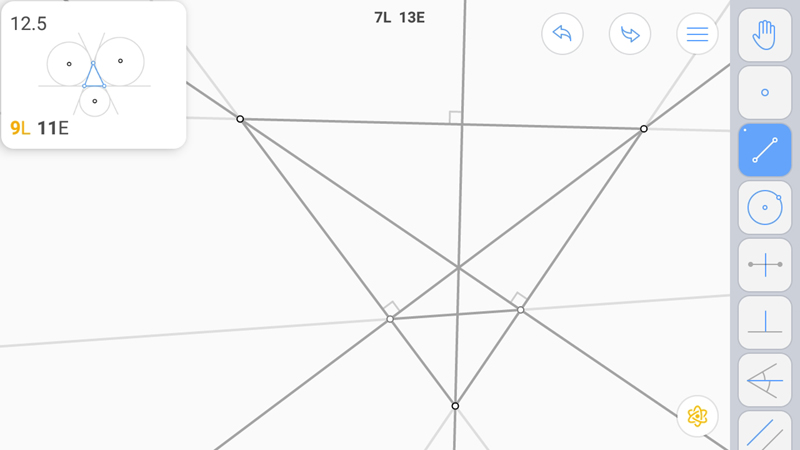
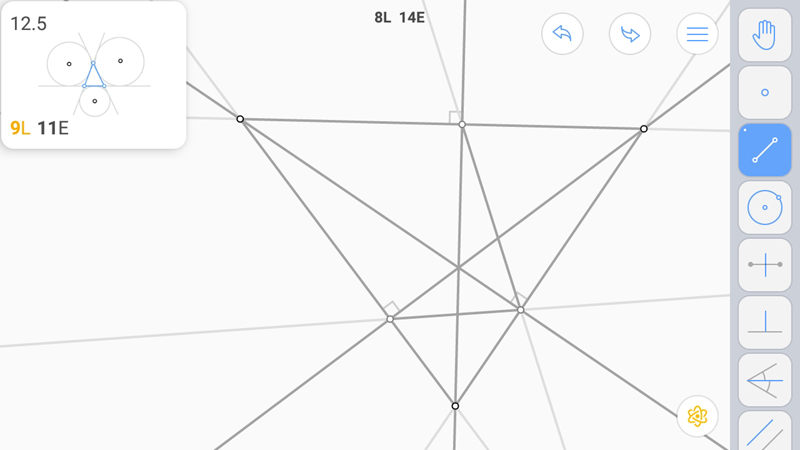
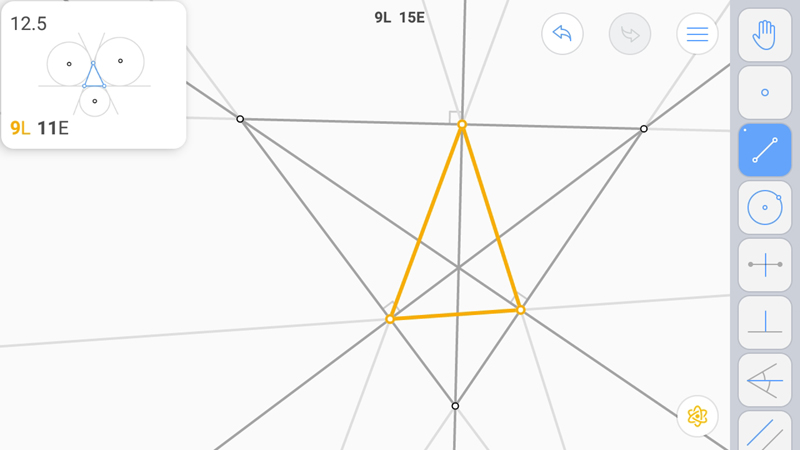
L-звезда. Решение одно.
slider_L
E-решения пока нет.

