Задача : Альфа 1.7
Квадрат, вписанный в окружность
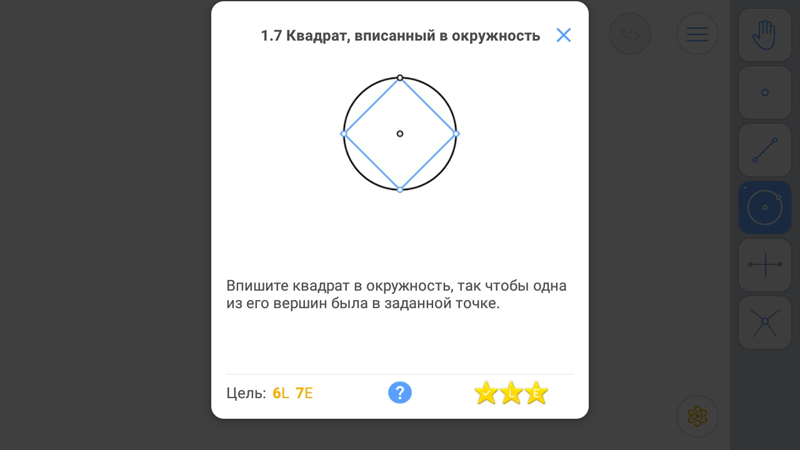
Известно:
Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и являются биссектрисами углов.
Поскольку у нас задана точка-вершина и центр окружности, то можно построить диаметр, что даст противоположную вершину, и серединный перпендикуляр к диаметру. Точки пересечения серединного перпендикуляра с окружностью дадут нам еще две вершины квадрата.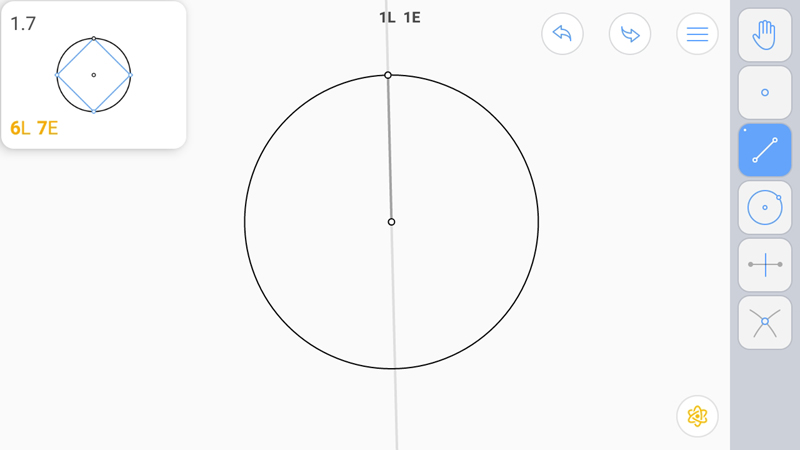
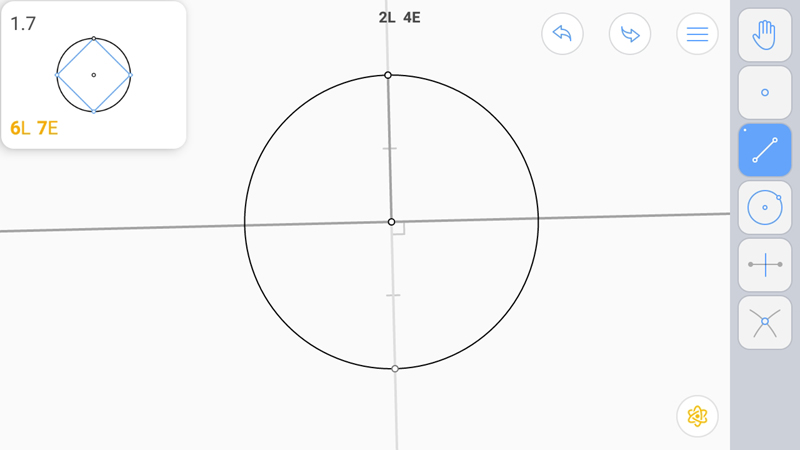
И построим стороны.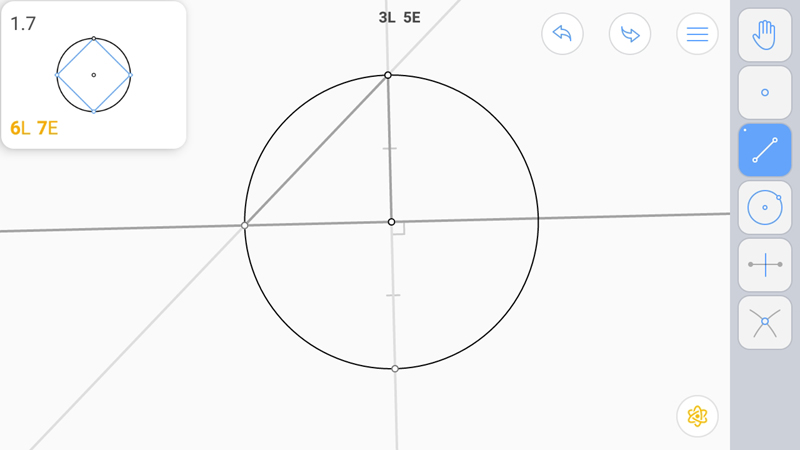
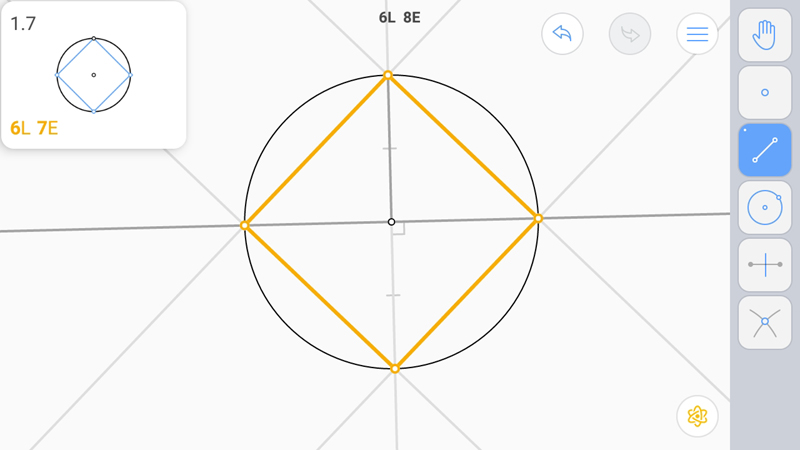
L-звезда.
slider_L
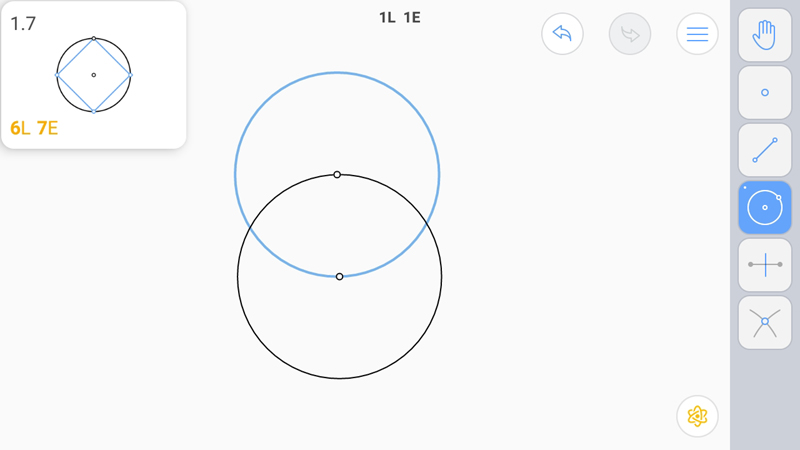
Решение на E-звезду совершенно не очевидное. Для построения нам понадобится вспомогательная "окружность-наседка", построенная на точках пересечения окружности и ее "сестры" равного радиуса, проведенной из точки на первой окружности. Эта окружность еще не раз поможет нам в построениях в других задачах.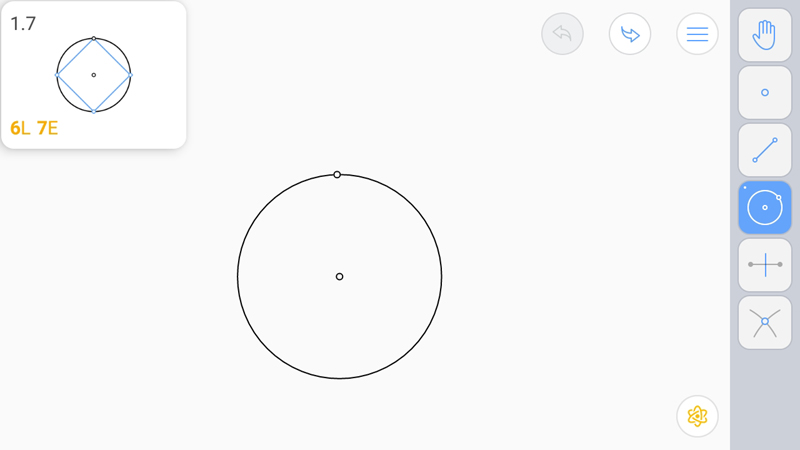
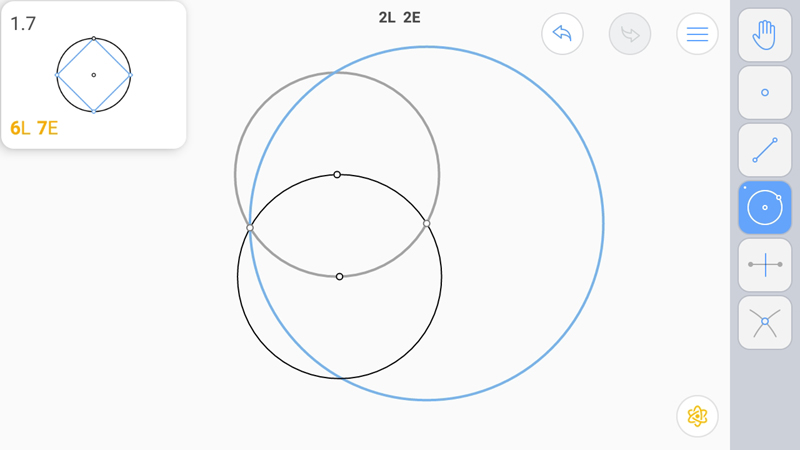
Точка пересечения вспомогательной прямой, проходящей через центр первой окружности с центром вспомогательной окружности даст нам возможность получить прямую, проходящую под углом 45 градусов к диаметру исходной окружности, проведенному через начальную точку.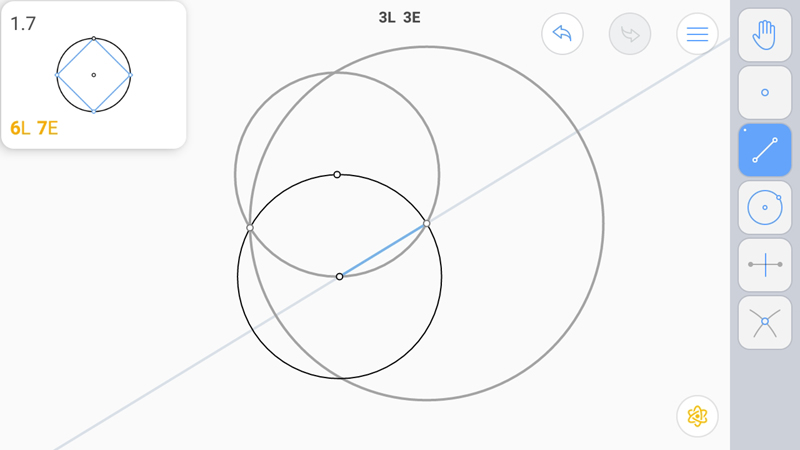
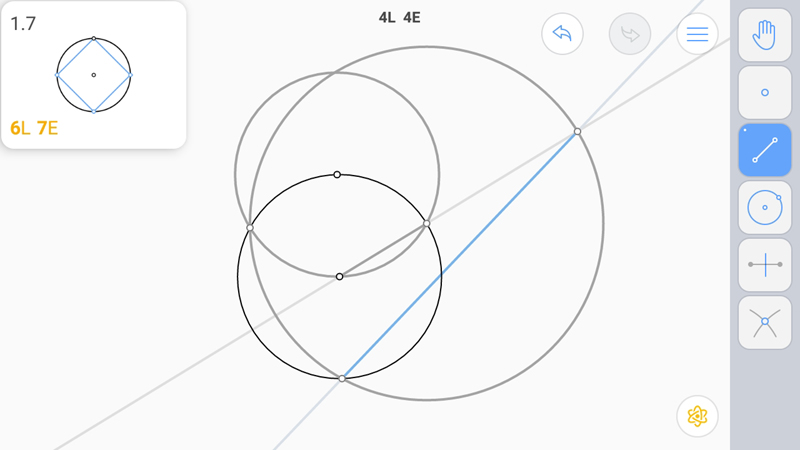
А вторая точка пересечения вспомогательной прямой и вспомогательной окружности даст угол 45 градусов с другой стороны.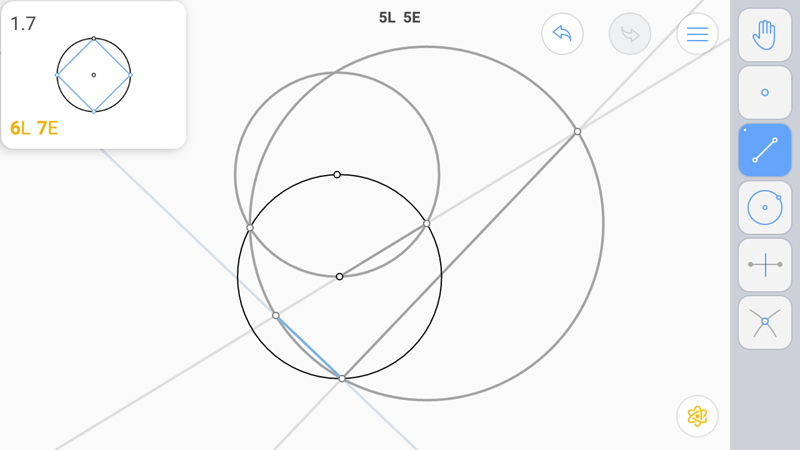
Осталось достроить квадрат.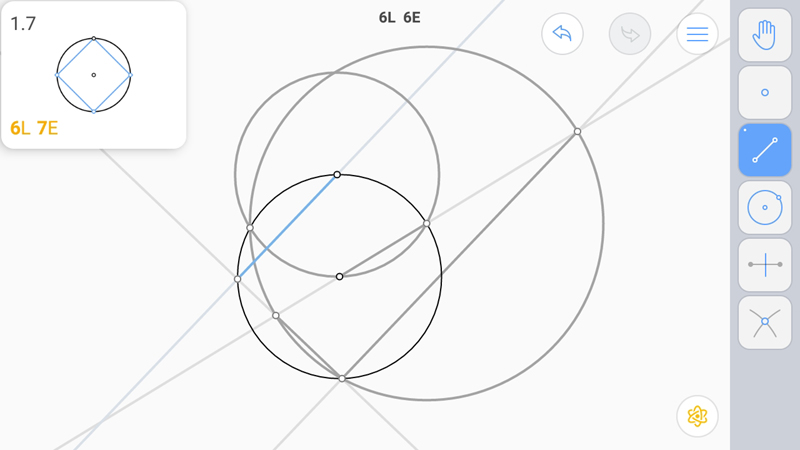
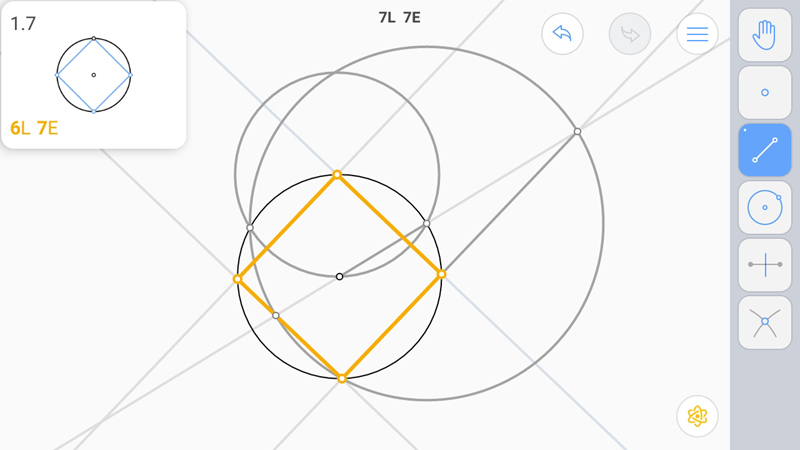
E-звезда. Такой квадрат единственный. Получили выход на Бету.
slider_E
Геометрическое обоснование правильности решения.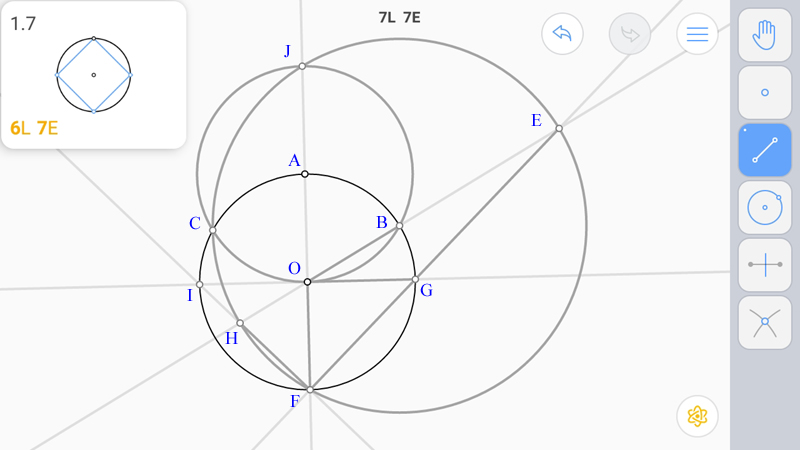
Построим перпендикуляр OG к OA.
Мы уже видели построение угла 60°. Если посмотреть на пересечение окружностей О и А, то дуга BC окружности О составляет 120°, два по 60°.
Окружность В отмеривает данную дугу в дугу BF, тоже 120°. Оставшаяся дуга CF также составляет 120° (360°-2*120°).
На будущее отсюда можно увидеть, что точки пересечения J и F окружности В с окружностями О и А лежат на прямой АО, так как дуга AF составляет 60°+120°=180°.
Центральная дуга CF окружности О составляет 120°, вписанный угол CBF будет вдвое меньше, 60°. Но центральный угол окружности В, опирающийся на эту же дугу также будет иметь угол 60°. Значит, вписанный угол CEF составит 30°, а угол HEF, как половина, равен 15°.
Поскольку угол AOB равен 60°, а AOG прямой, значит, угол BOG равен 30° (90°-60°=30°).
В треугольнике OFE угол EOF равен 30°+90°=120°, OEF как уже выяснили 15°, значит, угол OFE составит 180°-120°-15°=45°.
Но поскольку угол HFE вписанный и опирается на диаметр окружности B, то он прямой. Значит, угол HFO также составляет 45°.

