Задача : Альфа 1.6
Центр окружности
Известно:
Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде.
Если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам.
Нужны две хорды и серединные перпендикуляры к ним, которые выполнят роль радиусов. Радиусы-серединные перпендикуляры пересекутся в центре окружности. Но сами хорды для построения серединных перпендикуляров при этом строить не требуется.
Построим серединные перпендикуляры к произвольным точкам на окружности. В точке их пересечения будет центр окружности.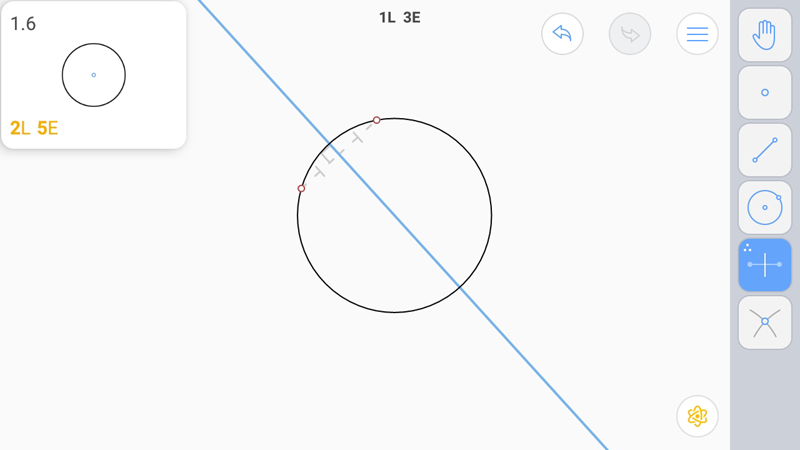
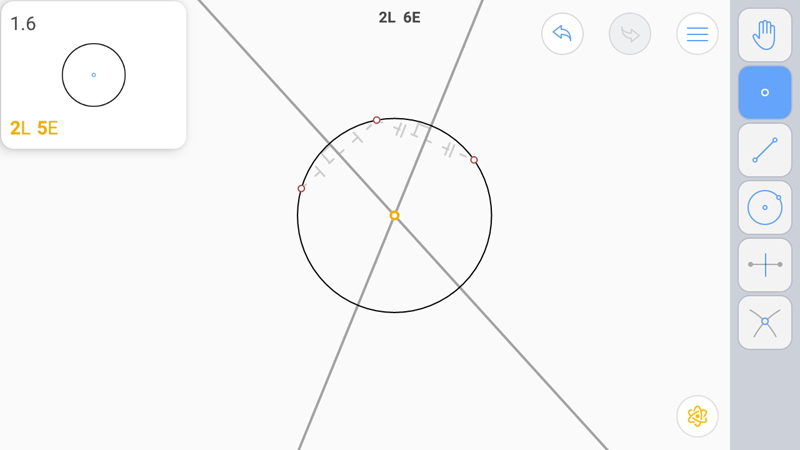
L-звезда.
slider_L
Для получения E-звезды надо построить два серединных перпендикуляра, используя общую вспомогательную окружность, чтобы сократить число действий. Построим первый серединный перпендикуляр.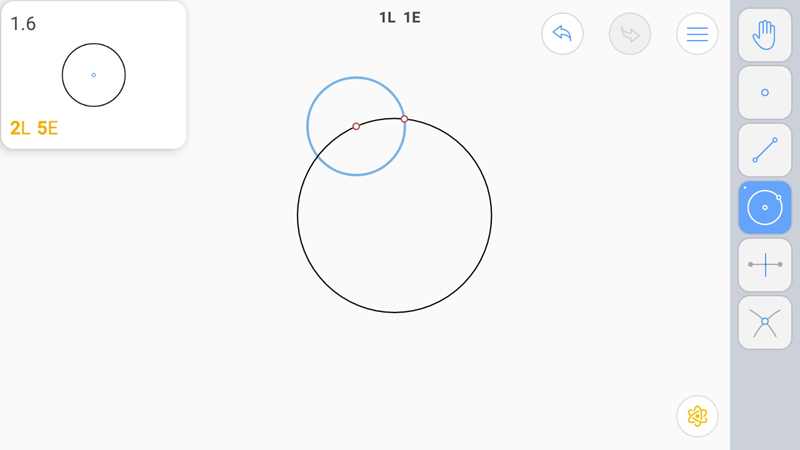
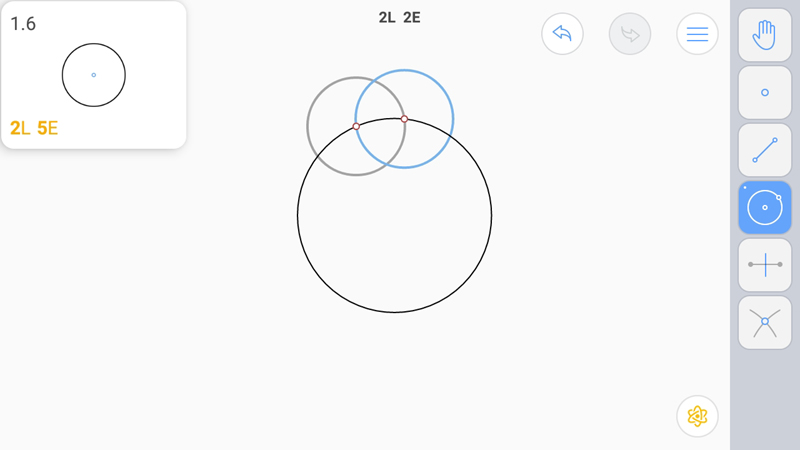
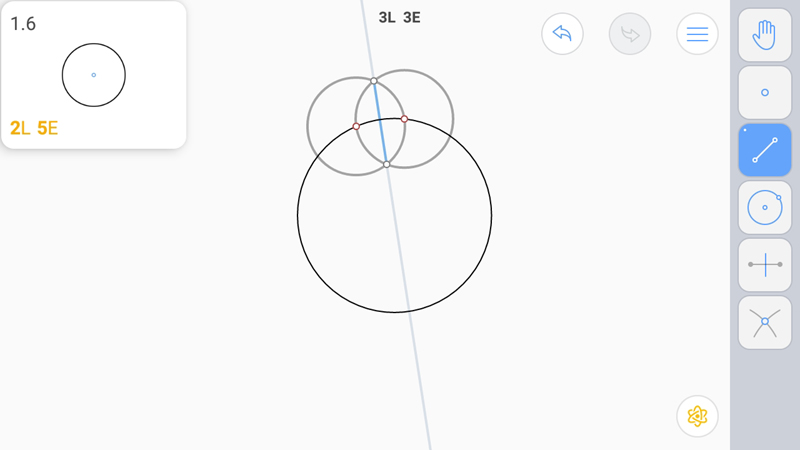
Теперь построим второй серединный перпендикуляр, используя первую вспомогательную окружность.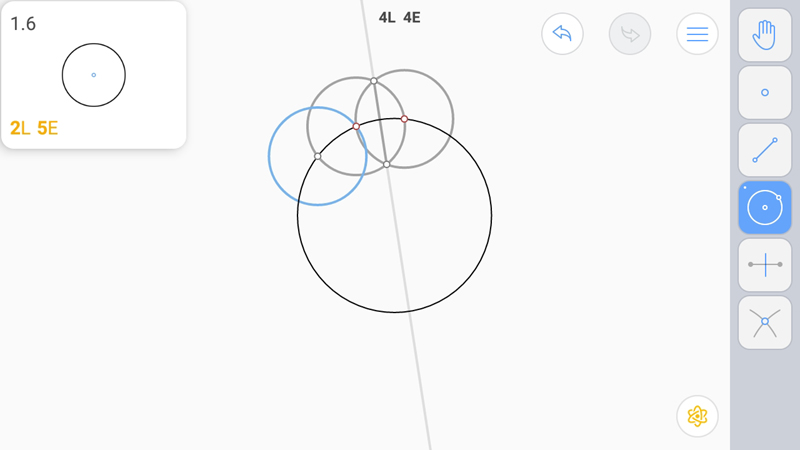
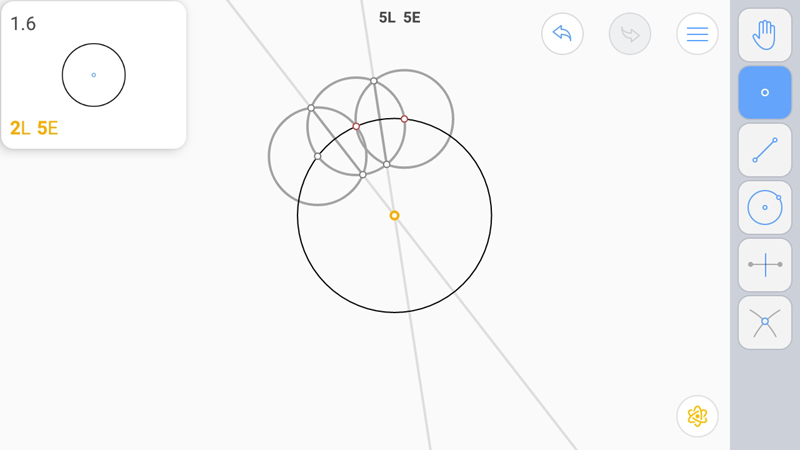
E-звезда. Очевидно, что центр окружности единственный.
slider_E

