Задача : Альфа 1.4
Окружность, вписанная в квадрат
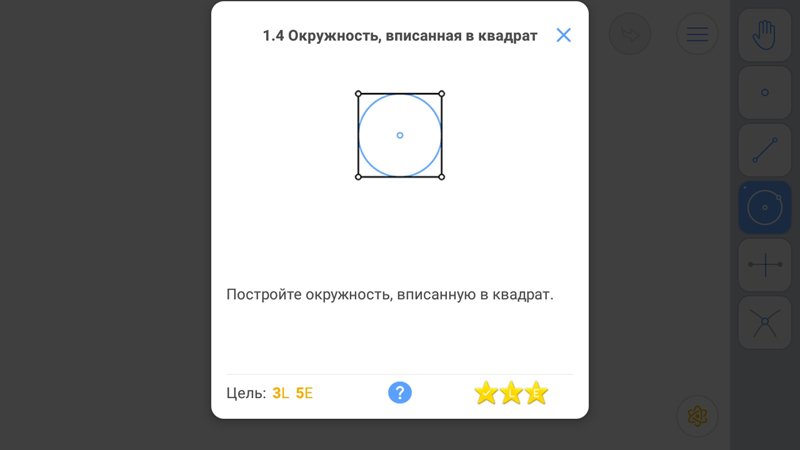
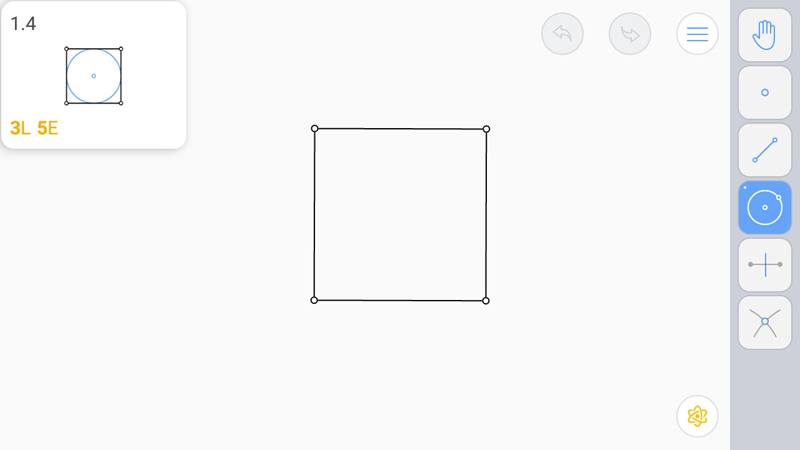
Известно:
Центр вписанной окружности есть точка пересечения биссектрис углов.
В квадрате центр вписанной окружности совпадает с центром описанной окружности и точкой пересечения серединных перпендикуляров к сторонам.
Нужно найти центр вписанной окружности квадрата и по меньшей мере середину одной стороны, чтобы провести туда окружность.
Середину стороны даст серединный перпендикуляр, их пересечение даст центр вписанной окружности квадрата.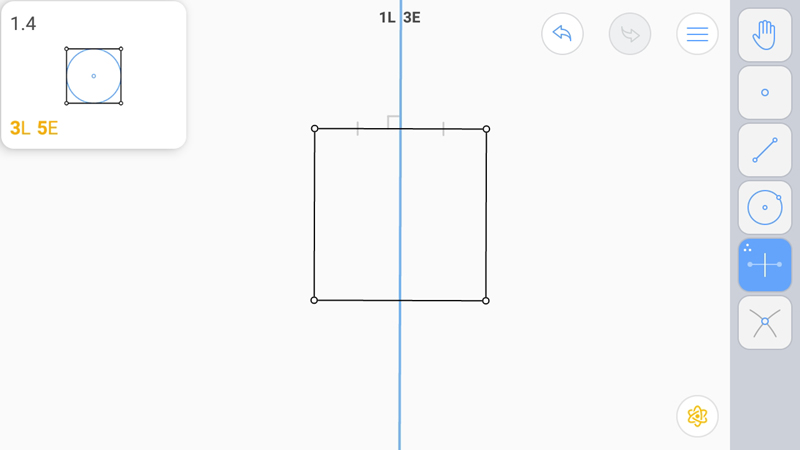
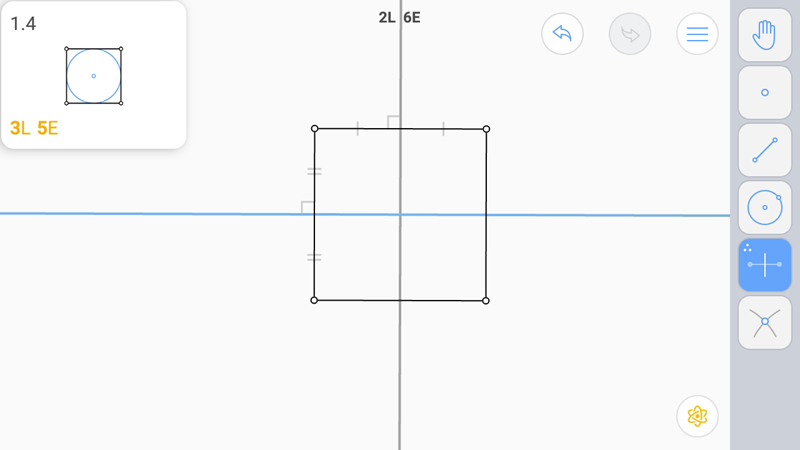
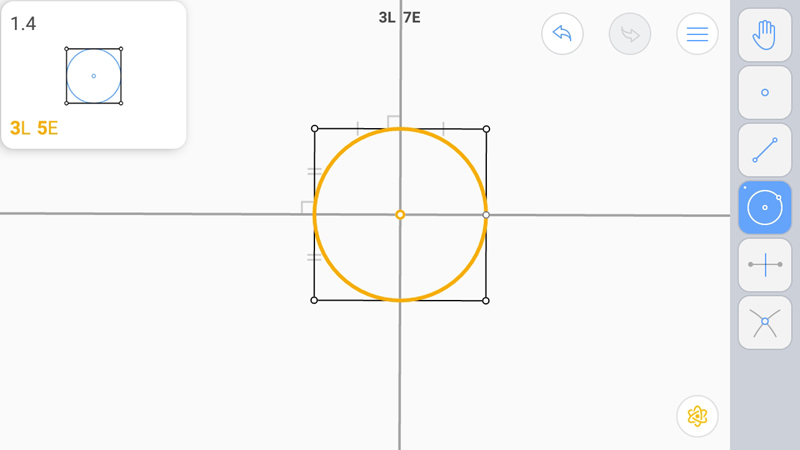
L-звезда.
slider_L
Поскольку центр квадрата есть точка пересечения диагоналей и серединных перпендикуляров к сторонам, то для получения E-звезды построим одну диагональ и один серединный перпендикуляр. Это даст нам обе нужные точки для построения вписанной окружности.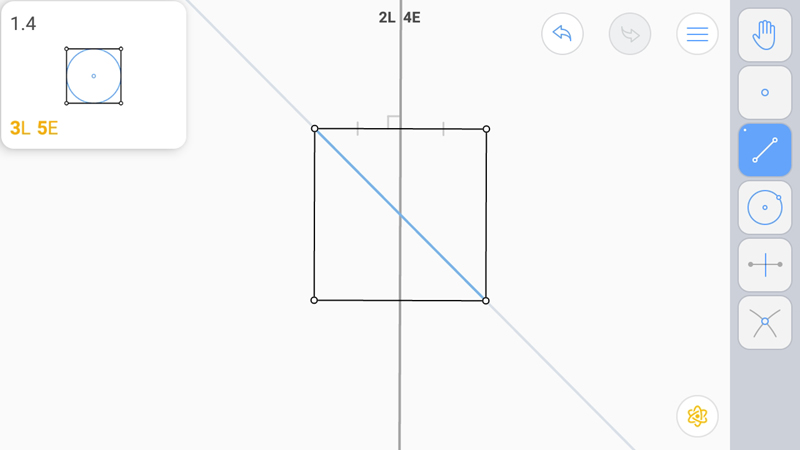
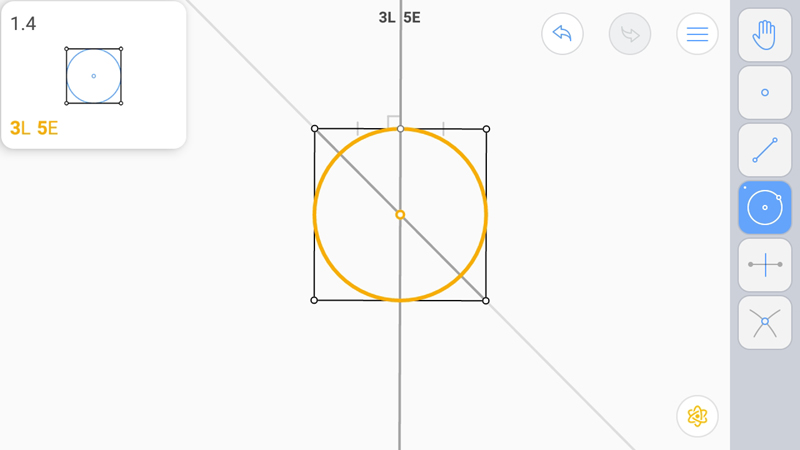
E-звезда. Одновременно и L-звезда. Других решений нет.
slider_E

