Задача : Альфа 1.2
Серединный перпендикуляр
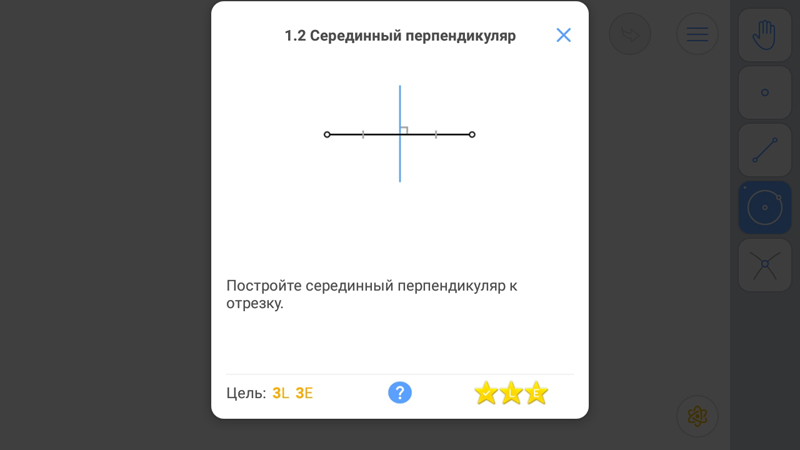
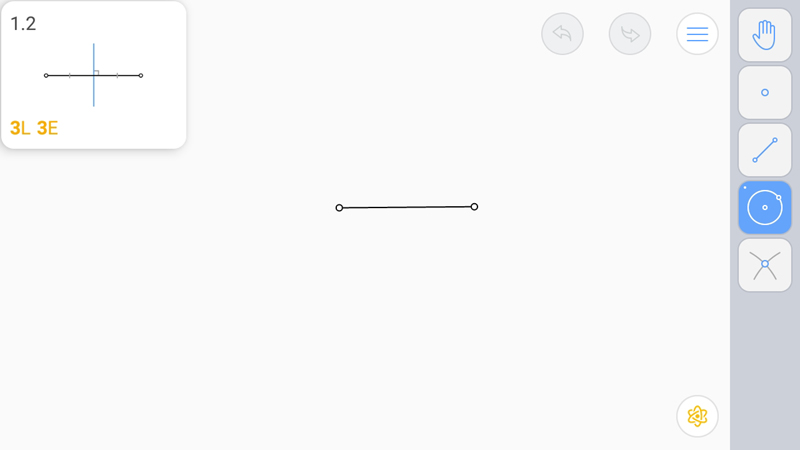
Известно:
- Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
- Обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Для построения серединного перпендикуляра проводим две окружности равных радиусов с центрами в концах отрезков. Поскольку инструмента построения окружности заданного радиуса нет, строим окружности с радиусом равным отрезку (из одного конца отрезка в другой и навстречу из второго в первый), и соединяем точки пересечения окружностей. Нужно заметить, что такое построение как "встречные окружности" применяется очень часто.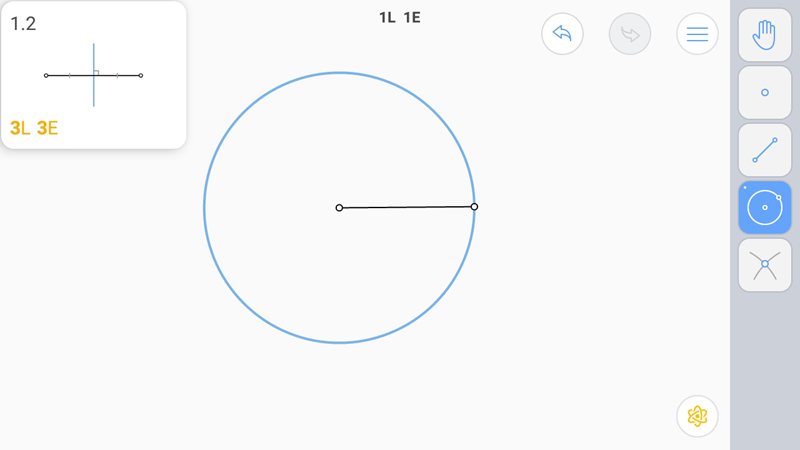
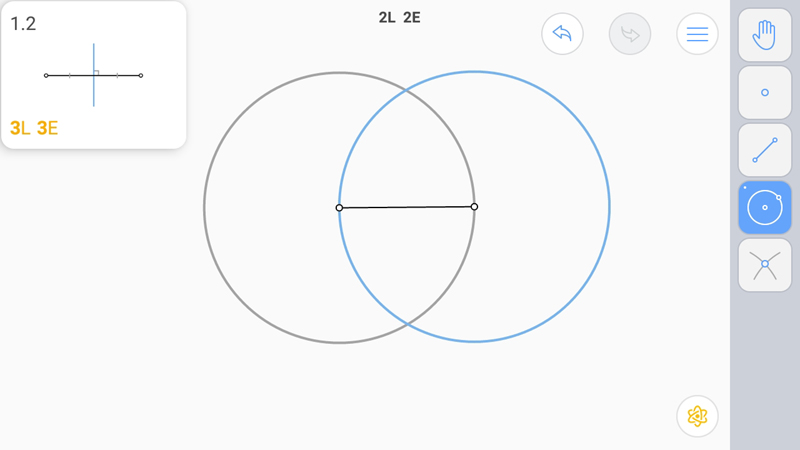
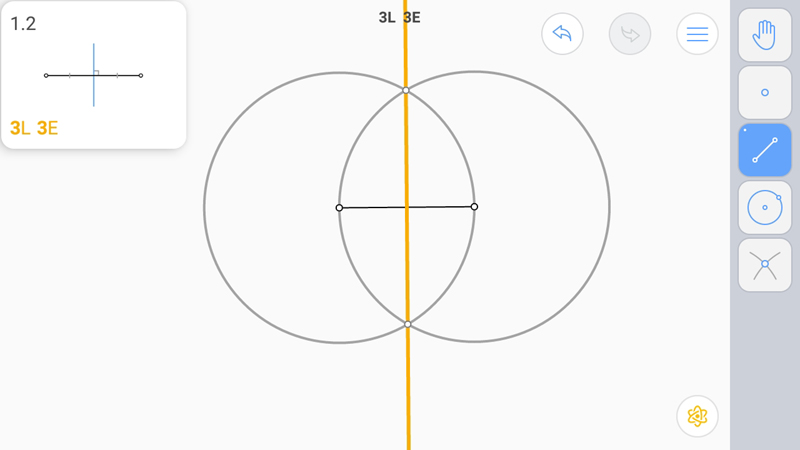
Точки пересечения равноудалены от концов отрезка, значит, лежат на серединном перпендикуляре. А поскольку через две точки можно провести только одну прямую, то прямая, их соединяющая и есть серединный перпендикуляр.
L и E звезды. Серединный перпендикуляр может быть только один, V-звезды быть не может.
slider_L
У нас появился новый инструмент - серединный перпендикуляр. Стоит три элементарных действия.

